Maller's optimization for Kimchi

This document proposes a protocol change for kimchi.

What is Maller's optimization?

See the section on Maller's optimization for background.

Overview

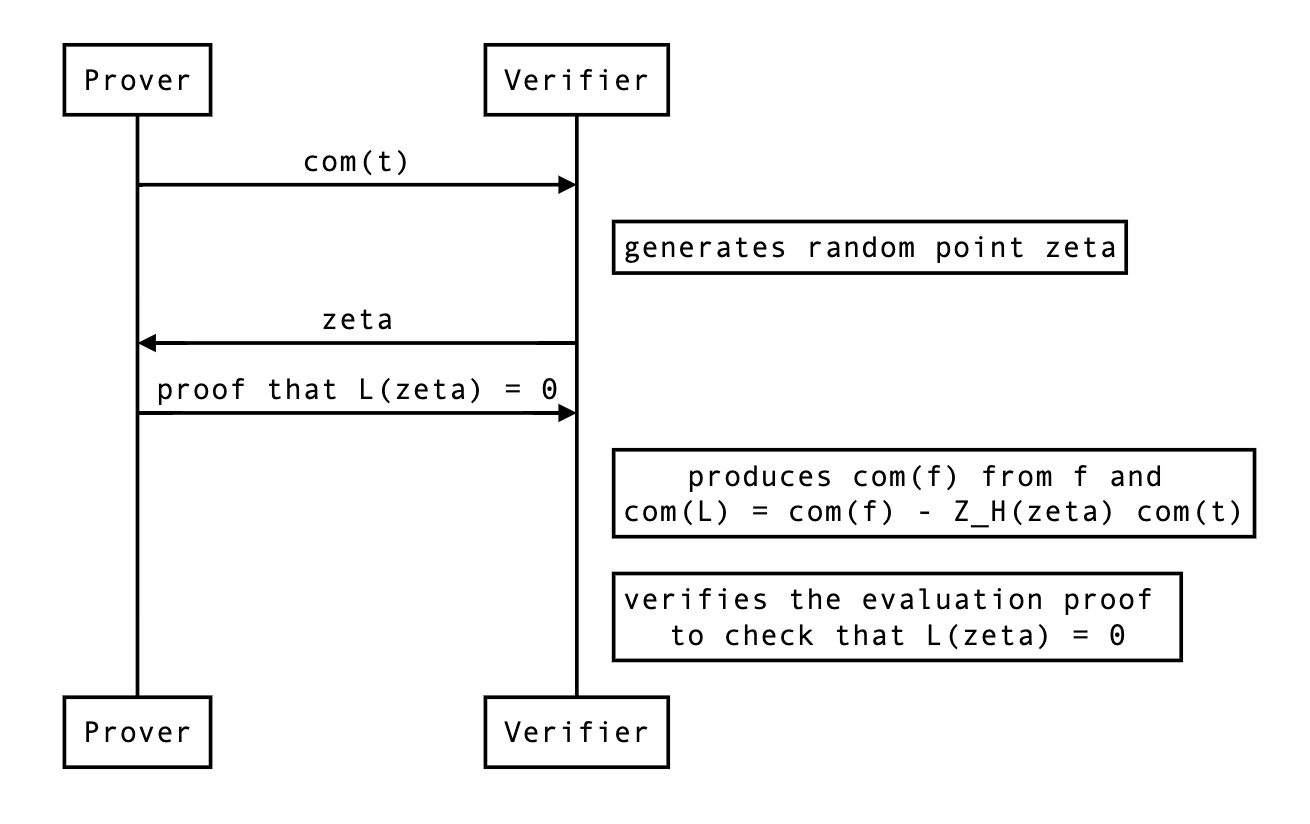
We want the verifier to form commitment to the following polynomial:

$$L(x) = f(x) - Z_H(\zeta) \cdot t(x)$$

They could do this like so:

$$\mathsf{com}(L) = \mathsf{com}(f) - Z_H(\zeta) \cdot \mathsf{com}(t)$$

Since they already know $f$, they can produce $\mathsf{com}(f)$, the only thing they need is $\mathsf{com}(t)$. So the protocol looks like that:

In the rest of this document, we review the details and considerations needed to implement this change in kimchi.

How to deal with a chunked $t$?

There's one challenge that prevents us from directly using this approach: $\mathsf{com}(t)$ is typically sent and received in several commitments (called chunks or segments throughout the codebase). As $t$ is the largest polynomial, usually exceeding the size of the SRS (which is by default set to be the size of the domain).

The verifier side

Thus, the verifier will have to produce split commitments of $L$ and combine them with powers of $\zeta^n$ to verify an evaluation proof. Let's define $L$ as:

$$L = L_0 + x^n L_1 + x^{2n} L_1 + \cdots$$

where every $L_i$ is of degree $n-1$ at most. Then we have that

$$\mathsf{com}(L) = \mathsf{com}(L_0) + \mathsf{com}(x^n \cdot L_1) + \mathsf{com}(x^{2n} \cdot L_2) + \cdots$$

Which the verifier can't produce because of the powers of $x^n$, but we can linearize it as we already know which $x$ we're going to evaluate that polynomial with:

$$\mathsf{com}(\tilde L) = \mathsf{com}(L_0) + \zeta^n \cdot \mathsf{com}(L_1) + \zeta^{2n} \cdot \mathsf{com}(L_2) + \cdots$$

The prover side

This means that the prover will produce evaluation proofs on the following linearized polynomial:

$$\tilde L(x) = 1 \cdot L_0(x) + \zeta^n \cdot L_1(x) + \zeta^{2n} \cdot L_2(x) + \cdots$$

which is the same as $L(x)$ only if evaluated at $\zeta$. As the previous section pointed out, we will need $\tilde L(\zeta \omega)$ and $\tilde L(\zeta \omega) \neq L(\zeta \omega)$.

Evaluation proof and blinding factors

To create an evaluation proof, the prover also needs to produce the blinding factor $r_{L}$ associated with the chunked commitment of:

$$\tilde L = \tilde f - (\zeta^n - 1) \tilde t$$

To compute it, there are two rules to follow:

• when two commitment are added together, their associated blinding factors get added as well: $\mathsf{com}(a) + \mathsf{com}(b) \implies r_a + r_b$
• when scaling a commitment, its blinding factor gets scaled too: $n \cdot \mathsf{com}(a) \implies n \cdot r_a$

As such, if we know $r_f$ and $r_t$, we can compute:

$$r_{\tilde L} = r_{\tilde f} + (\zeta^n-1) \cdot r_{\tilde t}$$

The prover knows the blinding factor of the commitment to $t$, as they committed to it. But what about $f$? They never commit to it really, and the verifier recreates it from scratch using:

1. The commitments we sent them. In the linearization process, the verifier actually gets rid of most prover commitments, except for the commitment to the last sigma commitment $S_{\sigma6}$. (TODO: link to the relevant part in the spec) As this commitment is public, it is not blinded.
2. The public commitments. Think commitment to selector polynomials or the public input polynomial. These commitments are not blinded, and thus do not impact the calculation of the blinding factor.
3. The evaluations we sent them. Instead of using commitments to the wires when recreating $f$, the verifier uses the (verified) evaluations of these in $\zeta$. If we scale our commitment $\mathsf{com}(z)$ with any of these scalars, we will have to do the same with $r_z$.

Thus, the blinding factor of $\tilde L$ is $(\zeta^n-1) \cdot r_{\tilde t}$.

The evaluation of $\tilde L$

The prover actually does not send a commitment to the full $f$ polynomial. As described in the last check section. The verifier will have to compute the evaluation of $\tilde L(\zeta)$ because it won't be zero. It should be equal to the following:

$$\begin{aligned} & \tilde f(\zeta) - \tilde t(\zeta)(\zeta^n - 1) = \\ & \frac{1 - z(\zeta)}{(\zeta - 1)(\zeta - \omega^{n-k})}\left[ \frac{(\zeta^n - 1)(\zeta - \omega^{n-k})}{n} \alpha^{\mathsf{PERM1}} + \frac{\omega^{n-k}(\zeta^n - 1)(\zeta - 1)}{n} \alpha^{\mathsf{PERM2}} \right] \\ & - \mathsf{pub}(\zeta) \\ & \; - z(\zeta) \cdot \mathsf{zkpm}(\zeta) \cdot \alpha^{\mathsf{PERM0}} \\ & \; \qquad \qquad \cdot (w[0](\zeta) + \beta \cdot \mathsf{shift}[0] \zeta + \gamma) \\ & \; \qquad \qquad \cdot (w[1](\zeta) + \beta \cdot \mathsf{shift}[1] \zeta + \gamma) \\ & \; \qquad \qquad \cdot (w[2](\zeta) + \beta \cdot \mathsf{shift}[2] \zeta + \gamma) \\ & \; \qquad \qquad \cdot (w[3](\zeta) + \beta \cdot \mathsf{shift}[3] \zeta + \gamma) \\ & \; \qquad \qquad \cdot (w[4](\zeta) + \beta \cdot \mathsf{shift}[4] \zeta + \gamma) \\ & \; \qquad \qquad \cdot (w[5](\zeta) + \beta \cdot \mathsf{shift}[5] \zeta + \gamma) \\ & \; \qquad \qquad \cdot (w[6](\zeta) + \beta \cdot \mathsf{shift}[6] \zeta + \gamma) \\ & \; + z(\zeta \omega) \cdot \mathsf{zkpm}(\zeta) \cdot \alpha^{\mathsf{PERM0}} \\ & \; \qquad \qquad \cdot (w[0](\zeta) + \beta \cdot \sigma[0](\zeta) + \gamma) \\ & \; \qquad \qquad \cdot (w[1](\zeta) + \beta \cdot \sigma[1](\zeta) + \gamma) \\ & \; \qquad \qquad \cdot (w[2](\zeta) + \beta \cdot \sigma[2](\zeta) + \gamma) \\ & \; \qquad \qquad \cdot (w[3](\zeta) + \beta \cdot \sigma[3](\zeta) + \gamma) \\ & \; \qquad \qquad \cdot (w[4](\zeta) + \beta \cdot \sigma[4](\zeta) + \gamma) \\ & \; \qquad \qquad \cdot (w[5](\zeta) + \beta \cdot \sigma[5](\zeta) + \gamma) \\ & \; \qquad \qquad \cdot (w[6](\zeta) + \gamma) + \end{aligned}$$

Because we use the inner product polynomial commitment, we also need:

$$\tilde L(\zeta \omega) = \tilde f(\zeta \omega) - Z_H(\zeta) \cdot \tilde t(\zeta \omega)$$

Notice the $Z_H(\zeta)$. That evaluation must be sent as part of the proof as well.

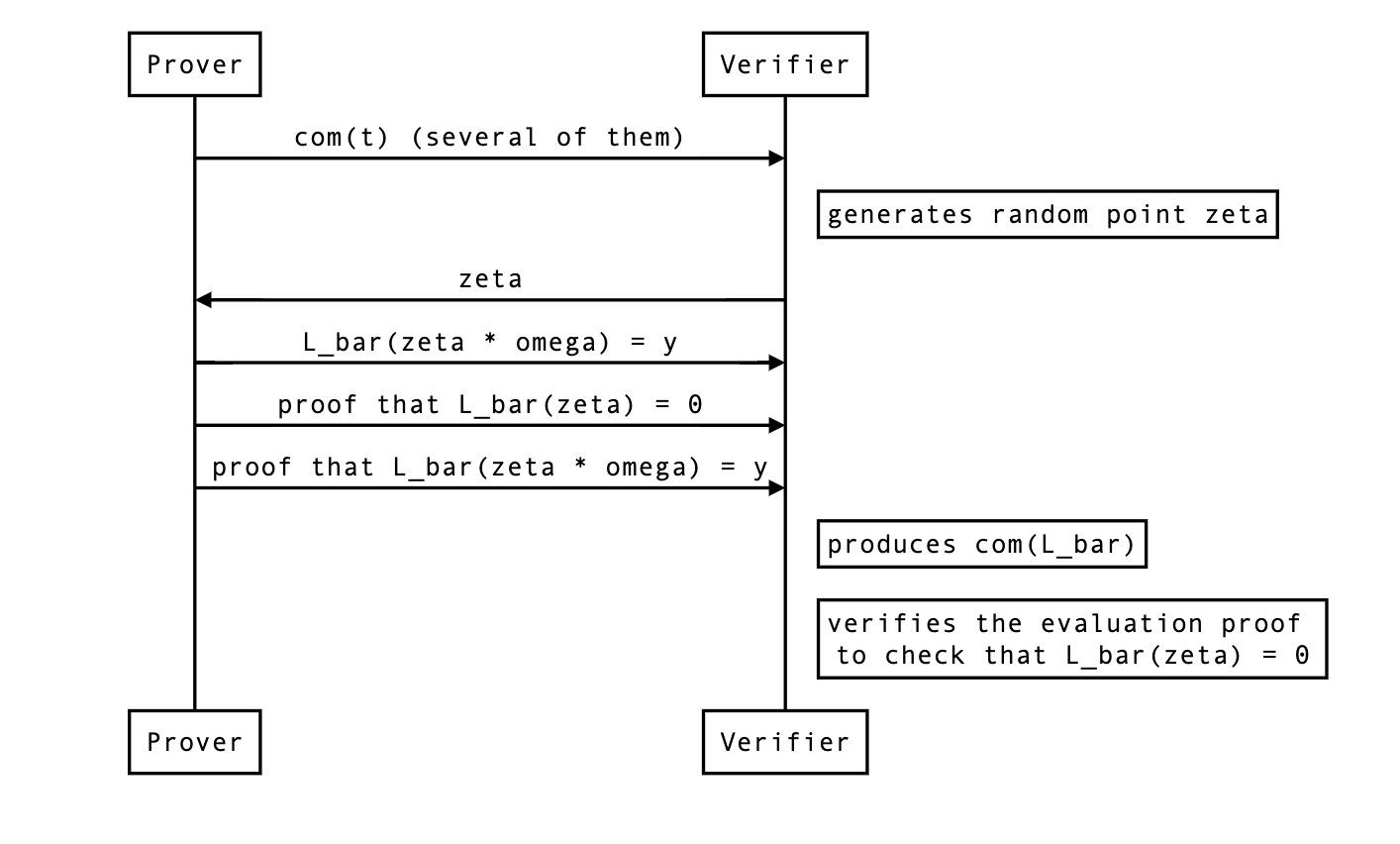
The actual protocol changes

Now here's how we need to modify the current protocol:

1. The evaluations $f(\zeta), f(\zeta \omega), t(\zeta), t(\zeta \omega)$ (and their corresponding evaluation proofs) don't have to be part of the protocol anymore.
2. The prover must still send the chunked commitments to $t$.
3. The prover must create a linearized polynomial $\tilde L$ by creating a linearized polynomial $\tilde f$ and a linearized polynomial $\tilde t$ and computing: $\tilde L = \tilde f + (\zeta^n-1) \cdot \tilde t$
4. While the verifier can compute the evaluation of $\tilde L(\zeta)$ by themselves, they don't know the evaluation of $\tilde L(\zeta \omega)$, so the prover needs to send that.
5. The verifier must recreate $\mathsf{com}(\tilde L)$, the commitment to $\tilde L$, themselves so that they can verify the evaluation proofs of both $\tilde L(\zeta)$ and $\tilde L(\zeta\omega)$.
6. The evaluation of $\tilde L(\zeta \omega)$ must be absorbed in both sponges (Fq and Fr).

The proposal is implemented in #150 with the following details:

• the $\tilde L$ polynomial is called ft.
• the evaluation of $\tilde L(\zeta)$ is called ft_eval0.
• the evaluation $\tilde L(\zeta\omega)$ is called ft_eval1.