Maller's Optimization to Reduce Proof Size

In the $\plonk$ paper, they make use of an optimization from Mary Maller in order to reduce the proof size.

Explanation

Maller's optimization is used in the "polynomial dance" between the prover and the verifier to reduce the number of openings the prover send.

Recall that the polynomial dance is the process where the verifier and the prover form polynomials together so that:

the prover doesn't leak anything important to the verifier
the verifier doesn't give the prover too much freedom

In the dance, the prover can additionally perform some steps that will keep the same properties but with reduced communication.

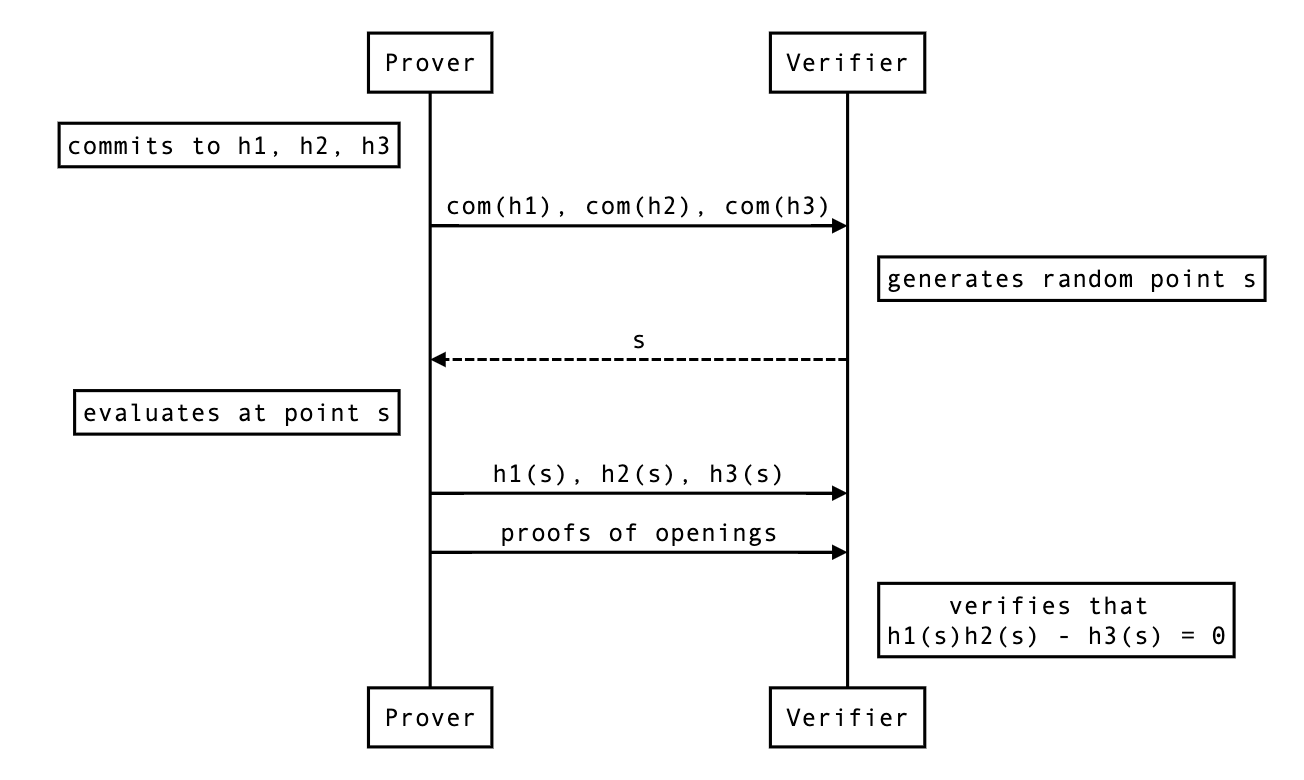
Let's see the protocol where Prover wants to prove to Verifier that

$\forall x \in \mathbb{F}, \; h_1(x)h_2(x) - h_3(x) = 0$

given commitments of $h_1, h_2, h_3$ ,

maller 1

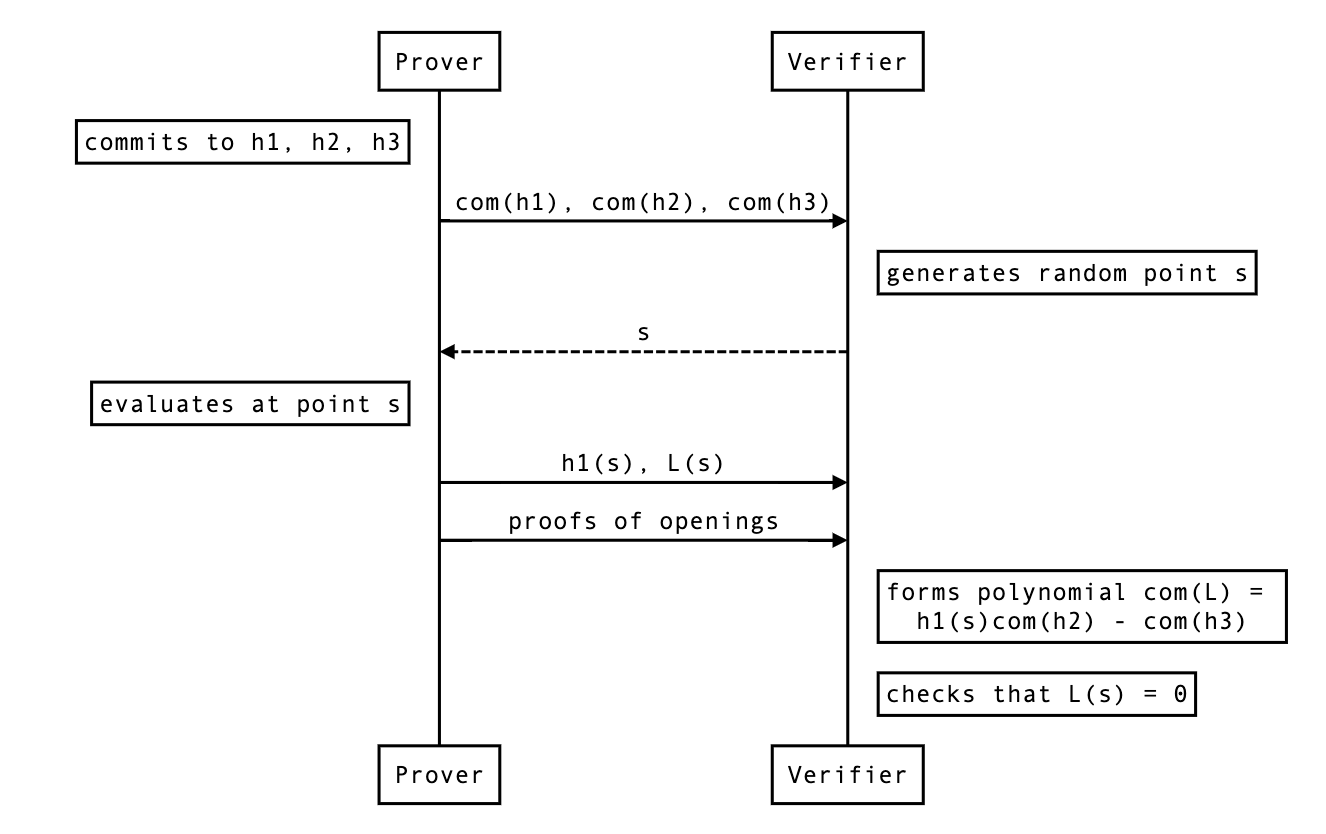
A shorter proof exists. Essentially, if the verifier already has the opening h1(s), they can reduce the problem to showing that

$\forall x \in \mathbb{F}, \; L(x) = h_1(s)h_2(x) - h_3(x) = 0$

given commitments of $h_1, h_2, h_3$ and evaluation of $h1$ at a point $s$ .

maller 2

Notes

Why couldn't the prover open the polynomial $L'$ directly?

$L'(x) = h_1(x)h_2(x) - h_3(x)$

By doing

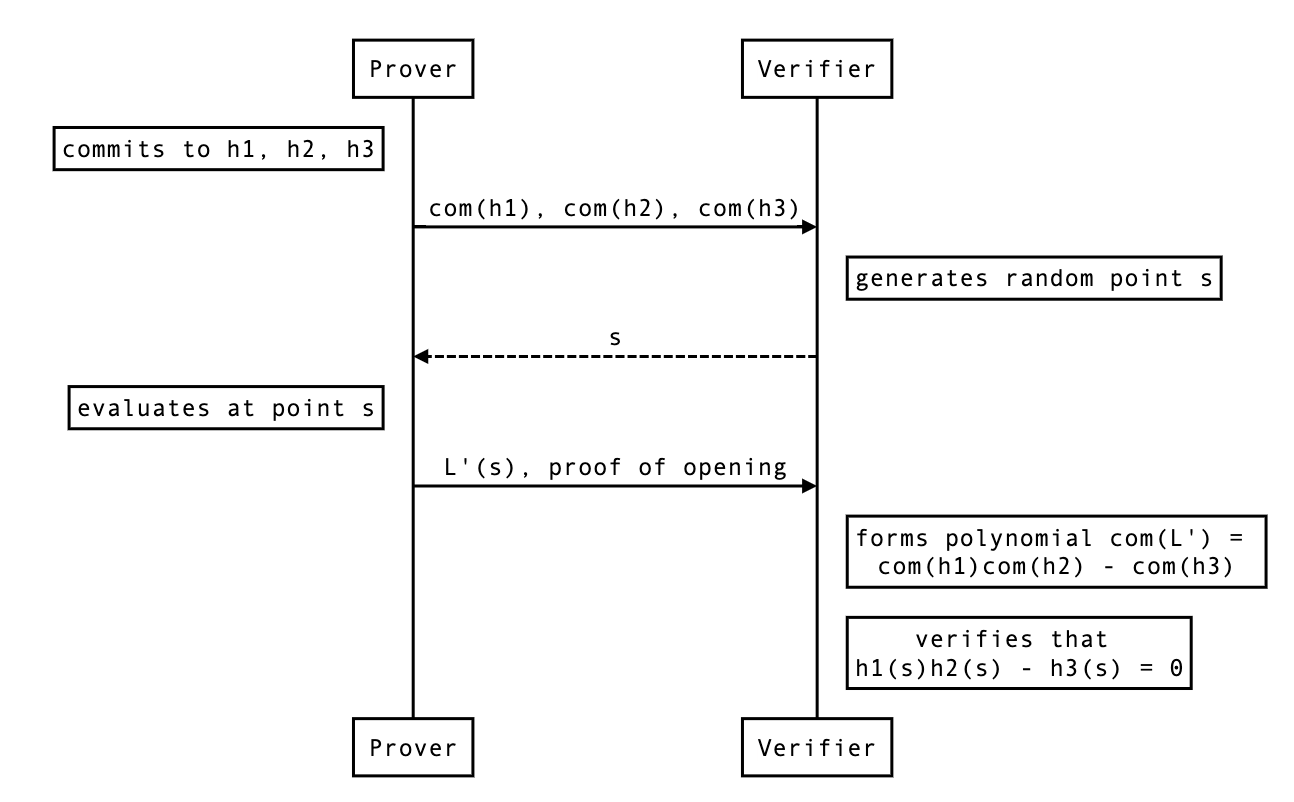
maller 3

The problem here is that you can't multiply the commitments together without using a pairing (if you're using a pairing-based polynomial commitment scheme), and you can only use that pairing once in the protocol.

If you're using an inner-product-based commitment, you can't even multiply commitments.

question: where does the multiplication of commitment occurs in the pairing-based protocol of $\plonk$ ? And how come we can use bootleproof if we need that multiplication of commitment?