$\plookup$

$\plookup$ allows us to check if witness values belong to a look up table. This is usually useful for reducing the number of constraints needed for bit-wise operations. So in the rest of this document we'll use the XOR table as an example.

A	B	Y
0	0	0
0	1	1
1	0	1
1	1	0

First, let's define some terms:

• lookup table: a table of values that means something, like the XOR table above
• joint lookup table: a table where cols have been joined together in a single col (with a challenge)
• table entry: a cell in a joint lookup table
• single lookup value: a value we're trying to look up in a table
• joint lookup values: several values that have been joined together (with a challenge)

A joint lookup table looks like this, for some challenge $\alpha$:

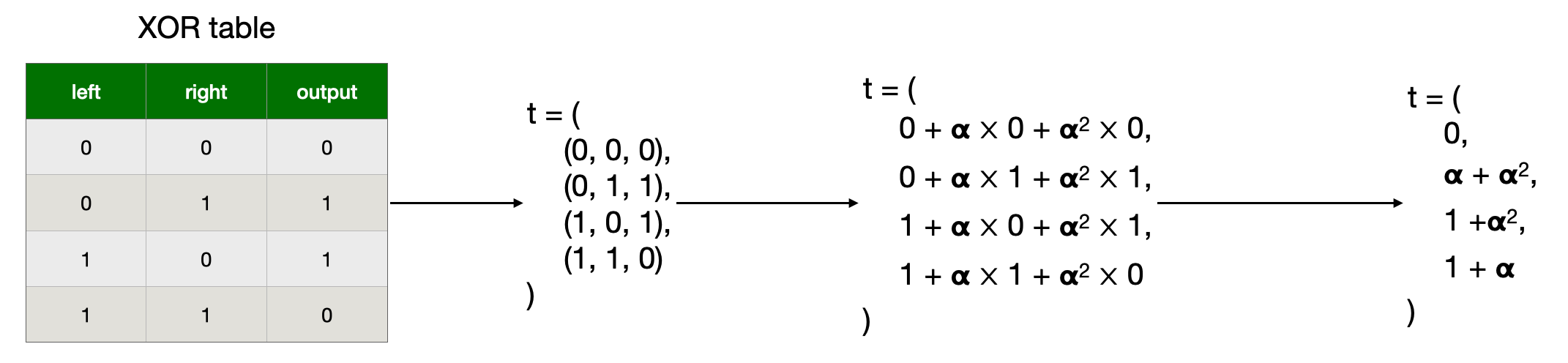
Constraints

Computes the aggregation polynomial for maximum $n$ lookups per row, whose $k$-th entry is the product of terms:

$$\frac{(\gamma(1 + \beta) + t_i + \beta t_{i+1}) \prod_{j=0}^n ( (1 + \beta) (\gamma + f_{i,j}) )}{\prod_{j=0}^{n+1} (\gamma(1 + \beta) + s_{i,j} + \beta s_{i+1,j})}$$

for $i < k$.

• $t_i$ is the $i$-th entry in the table
• $f_{i, j}$ is the $j$-th lookup in the $i$-th row of the witness

For every instance of a value in $t_i$ and $f_{i,j}$, there is an instance of the same value in $s_{i,j}$

$s_{i,j}$ is sorted in the same order as $t_i$, increasing along the 'snake-shape'

Whenever the same value is in $s_{i,j}$ and $s_{i+1,j}$, that term in the denominator product becomes

$(1 + \beta) (\gamma + s_{i,j})$

this will cancel with the corresponding looked-up value in the witness

$(1 + \beta) (\gamma + f_{i,j})$

Whenever the values $s_{i,j}$ and $s_{i+1,j}$ differ, that term in the denominator product will cancel with some matching

$(\gamma(1 + \beta) + t_{i'} + \beta t_{i'+1})$

because the sorting is the same in $s$ and $t$.

There will be exactly the same number of these as the number of values in $t$ if $f$ only contains values from $t$. After multiplying all of the values, all of the terms will have cancelled if $s$ is a sorting of $f$ and $t$, and the final term will be $1$ because of the random choice of $\beta$ and $\gamma$, there is negligible probability that the terms will cancel if $s$ is not a sorting of $f$ and $t$

But because of the snakify:

• we are repeating an element between cols, we need to check that it's the same in a constraint
• we invert the direction, but that shouldn't matter

FAQ

• how do we do multiple lookups per row?
• how do we dismiss rows where there are no lookup?