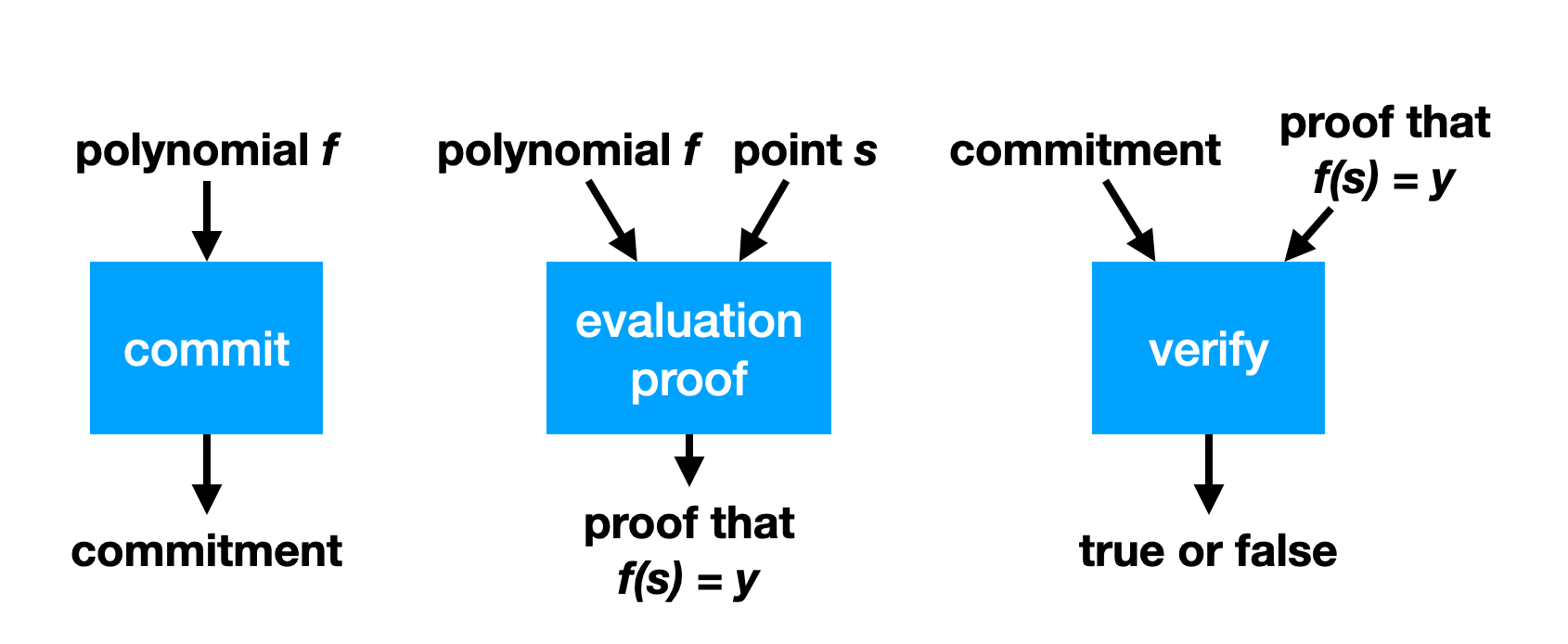
Polynomial commitments

A polynomial commitment is a scheme that allows you to commit to a polynomial (i.e. to its coefficients). Later, someone can ask you to evaluate the polynomial at some point and give them the result, which you can do as well as provide a proof of correct evaluation.

Schwartz-Zippel lemma

TODO: move this section where most relevant

Let $f(x)$ be a non-zero polynomial of degree $d$ over a field $\mathbb{F}$ of size $n$, then the probability that $f(s)=0$ for a randomly chosen $s$ is at most $\frac{d}{n}$.

In a similar fashion, two distinct degree $d$ polynomials $g(X)$ and $h(X)$ can at most intersect in $d$ points. This means that the probability that $g(s) = h(s)$ on a random $s\leftarrow \mathbb{F}$ is $\frac{d}{|\mathbb{F}|}$. This is a direct corollary of the Schwartz-Zipple lemma, because it is equivalent to the probability that $f(s) = 0$ with $f(X) = g(X) - h(X)$.